Derivazione delle funzioni iperboliche

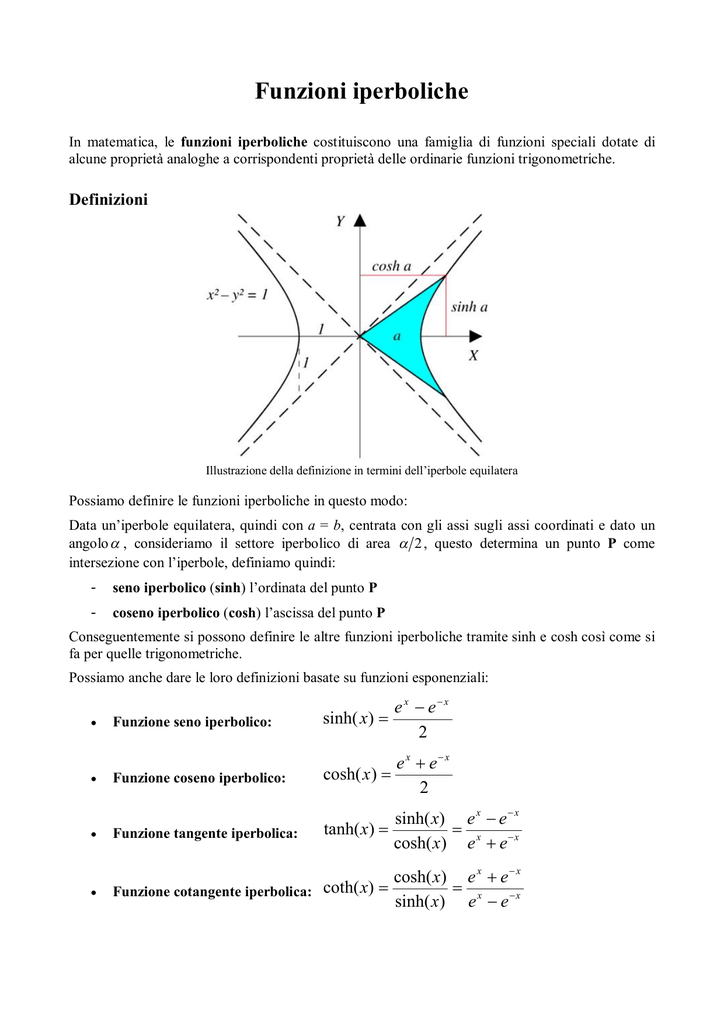
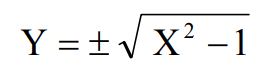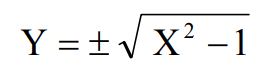L'equazione dell'iperbole equilatera in figura è:

${\displaystyle x^{2}-y^{2}=a^{2}}$

quindi:

${\displaystyle {\overline {OC}}=x,\qquad {\overline {PC}}={\sqrt {x^{2}-a^{2}}},\qquad {\overline {OA}}=a.}$

L'area del settore iperbolico ${\displaystyle OAP}$ è uguale all'area del triangolo ${\displaystyle OPC}$ meno l'area della regione del piano delimitata dall'arco di iperbole ${\displaystyle AP}$, dall'asse delle ${\displaystyle x}$ e dal segmento ${\displaystyle PC.}$

${\displaystyle S={\frac {1}{2}}x{\sqrt {x^{2}-a^{2}}}-\int _{a}^{x}{\sqrt {t^{2}-a^{2}}}\,dt={\frac {a^{2}}{2}}\left[\ln \left(x {\sqrt {x^{2}-a^{2}}}\right)-\ln a\right]={\frac {a^{2}}{2}}\left[\ln \left({\frac {x}{a}} {\sqrt {\left({\frac {x}{a}}\right)^{2}-1}}\right)\right].}$

Posto ${\displaystyle {\frac {2S}{a^{2}}}=t}$, si ha:

${\displaystyle \ln \left({\frac {x}{a}} {\sqrt {\left({\frac {x}{a}}\right)^{2}-1}}\right)=t}$

${\displaystyle {\frac {x}{a}} {\sqrt {\left({\frac {x}{a}}\right)^{2}-1}}=e^{t}}$

${\displaystyle \left({\frac {x}{a}}\right)^{2}-1=\left(e^{t}-{\frac {x}{a}}\right)^{2}}$

${\displaystyle 2{\frac {x}{a}}e^{t}=e^{2t} 1}$

${\displaystyle {\frac {x}{a}}={\frac {e^{t} e^{-t}}{2}}.}$

Quest'ultima relazione definisce il coseno iperbolico di ${\displaystyle t,}$ ${\displaystyle \cosh t}$.

${\displaystyle \cosh t={\frac {e^{t} e^{-t}}{2}}.}$

Si definisce inoltre il seno iperbolico:

${\displaystyle \sinh t={\frac {y}{a}}={\frac {\sqrt {x^{2}-a^{2}}}{a}}={\sqrt {\left({\frac {e^{t} e^{-t}}{2}}\right)^{2}-1}}={\sqrt {\left({\frac {e^{t}-e^{-t}}{2}}\right)^{2}}}={\frac {e^{t}-e^{-t}}{2}}.}$

L'argomento delle funzioni iperboliche è analogo a quello delle funzioni goniometriche se si considera che, nel caso della circonferenza, l'angolo, in radianti, è uguale al doppio dell'area del settore circolare diviso il raggio al quadrato:

${\displaystyle \theta ={\frac {2S}{a^{2}}}}$

e

${\displaystyle \cos \theta ={\frac {x}{a}},\qquad \sin \theta ={\frac {y}{a}}.}$